一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项）

1. 以下IP地址中错误的是 {{ select(1) }}

• 114.114.114.114
• 192.168.0.114
• 256.134.378.114
• 129.30.1.14

2. 考虑对n个数进行排序，以下最坏时问复杂度最低的排序方法是 {{ select(2) }}

• 插入排序
• 冒泡排序
• 归并排序
• 快速排序

3. 用0, 1, 1, 4, 5能组成多少个小于4000的自然数 {{ select(3) }}

• 138
• 57
• 53
• 104

4. 关于结构体，以下选项中描述错误的是 {{ select(4) }}

• 结构体类似类，每一个结构体对象可以集成多个属性
• 定义结构体时需要在语句末尾添加分号
• 可以重写结构体的运算方法
• 因为其面向对象的特征，结构体只在C++语言中存在

5. 下列Linux命令不能查看文件内容的是 {{ select(5) }}

• tail
• nano
• touch
• vim

6. 下列选项中硬件读写速度最快的是 {{ select(6) }}

• Cache
• 硬盘
• 内存（RAM）
• 寄存器

7. 八位有符号二进制数反码01011011的原码是 {{ select(7) }}

• 01011011
• 10100100
• 10100101
• 11010110

8. 以下程序当输入3时会输出

   # include <bits/stdc++.h>
   using namespace std;
   int main() {
   	int n, i = 1;
   	cin >> n;
   	do {
   		n *= (i <= 0 ? -1 : 2);
   		i += (n - 8) / 2;
   	} while (i >= 12);
   	cout << n;
   	return 0;
   }
   

   {{ select(8) }}

• 3
• -6
• 6
• 12

9. G 是一张有 n 个点 m 条边的连通图，必须删去（ ）条边才能将其变成一棵 n 节点的树 {{ select(9) }}

• 1
• m-n-1
• m+n-1
• m-n+1

10. 元素 R1、R2、R3、R4、R5 入栈的顺序为 R1、R2、R3、R4、R5。如果第一个出栈的是R3，那么第 5 个出栈的不可能是（ ）。 {{ select(10) }}

• R1
• R2
• R4
• R5

11. 前缀表达式 “+3 * 2 + 5 12” 的值是（ ）。 {{ select(11) }}

• 23
• 25
• 37
• 65

12. 一棵二叉树的中序遍历是EDFBACGJHK，先序遍历时ABDEFCGHJK，则这科二叉树的后序遍历是 {{ select(12) }}

• EFBDJKHGCA
• EFBJDKGHCA
• EFDBJKHGCA
• ADEBFGCHJK

13. A, B, C, D, E 在文中出现的频率分别是10%, 25%, 30%, 15%, 40%，若绘制成哈夫曼树，则A的哈夫曼编码应当是 {{ select(13) }}

• 01
• 0110
• 001
• 1

14. 一棵二叉树共有51个节点，设根结点高度为1，二叉树的深度为h，则该二叉树叶节点的数量为 {{ select(14) }}

• $\frac{(2^h-1) - 51}{2}+(51-2^{h-1}+1)$
• $\frac{2^h-51}{2}+(51-2^{h-1}-1)$
• $2^{h-1}-1-51+(51-2^h+1)$
• $2^{h-1}-1-51+(51-2^h-1)$

15. 老师和学生一起拍照片，老师站中间，4个男生和5个女生分别站在两边，相同性别的人必须站在一起，有多少种排列 {{ select(15) }}

• 4860
• 12250
• 7230
• 5760

二、阅读程序（程序输入不超过数组或字符串定义的范围；判断题正确填 T，错误填 F；除特殊说明外， 判断题1.5 分，选择题 3 分，共计 40 分）

阅读下面程序，完成第 16~21 题。

# include <bits/stdc++.h>
using namespace std;
int func1(int a, int b) {
  if (a <= b) return (a + b) / 2;
  if (b == 0) return 1;
  return func1(a+b, a*b) + func1(a-b, a/b);
}

int func2(int n, int m) {
  if (n > 2*m ) return n + m;
  return func2(func1(n, m), m+n);
}

int main() {
  int a, b;
  cin >> a >> b;
  cout << func2(a, b) << endl;
  cout << func1(a, b) << endl;
  return 0;
}

16. 如果删除第5行可能会有栈溢出的风险。（ ） {{ select(16) }}

• 正确
• 错误

17. 若输入的a, b相等，则输出的两行数值也相等（ ） {{ select(17) }}

• 正确
• 错误

18. 当a<b时，输出的第一行数值可能极大或极小。（ ） {{ select(18) }}

• 正确
• 错误

19. 当输入 a = 3，b = 1 时，程序输出的第一个值是 9，第二个值是 3。（ ） {{ select(19) }}

• 正确
• 错误

20. 若输入的字符串中 a 到 g 这 7 种字符均至少出现一次，如果希望输出结果为 no ，则输入的字符串长度至少为（ ）。 {{ select(20) }}

• 1
• 7
• 14
• 8

21. 这个程序最多正确输入并处理长度为（ ）的字符串 s 。 {{ select(21) }}

• 256
• 15
• 14
• 11

阅读下面程序，完成第 22~27 题。

22. 若输入的 X[1], X[2], ..., X[N ] 中有相同的数,程序会陷入死循环。（ ） {{ select(22) }}

• 正确
• 错误

23. 当且仅当输入的 X[1], X[2], … , X[N ] 全部相同时输出的两行结果相同。（ ） {{ select(23) }}

• 正确
• 错误

24. 该算法的原理是基数排序。（ ） {{ select(24) }}

• 正确
• 错误

25. （4分）若输入的 X[1], X[2], ..., X[N ] 互不相同，则下列说法正确的是（ ） {{ select(25) }}

• 输出的两行结果相同
• 将输出的第一行结果整体翻转后，将与第二行相同
• 将输出的第一行结果的第一项与最后一项交换后，将与第二行相同
• 以上说法都不正确

26. （4分）下列说法不正确的是（ ） {{ select(26) }}

• 输出的第一行即为将 X[1], X[2], ..., X[N ] 从小到大排序后得到的结果
• 输出的第二行即为将 X[1], X[2], ..., X[N ] 从大到小排序后得到的结果
• 若将 a[i]> a[j] 改为 a[i] >=a[j] ，则程序输出无变化
• 不存在时间复杂度更优的能与本程序达到相同目的的算法

27. 该程序的时间复杂度为（ ） {{ select(27) }}

• O(nlogn)
• O(n)
• O(n^2)
• O(n * √n )

阅读下面程序，完成第28~33题。

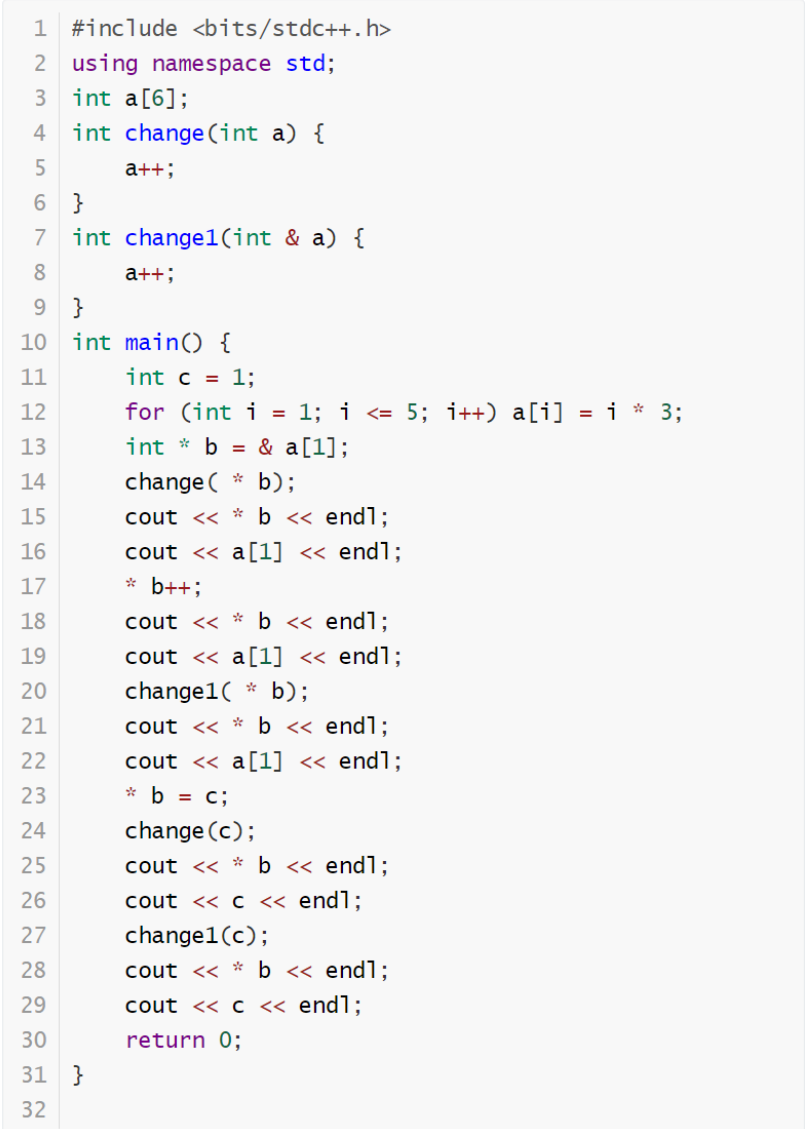
28. 将 int c = 1; 中 int 换为 long long 后程序依然能通过编译。（ ） {{ select(28) }}

• 正确
• 错误

29. change 与 change1 两个函数等价。（ ） {{ select(29) }}

• 正确
• 错误

30. 将 * b = c; 换为 b = &c; 输出值不变。（ ） {{ select(30) }}

• 正确
• 错误

31. 将 int * b = & a[1]; 换为 int * b=a+1; 输出值不变。（ ） {{ select(31) }}

• 正确
• 错误

32. 输出结果的最大值是。（ ） {{ select(32) }}

• 6
• 4
• 7
• 5

33. 输出结果的乘积是。（ ） {{ select(33) }}

• 13608
• 11520
• 5760
• 6804

三、完善程序（单选题，每小题3分，共计30分）

阅读下面题目，完成第 34 ∼ 38 题。

小帅目前处在一个二维平面上，初始状态下小帅在原点 (0, 0)。小帅会进行 n 次如下的移动，每次移动小帅有三种选择：

l 从 (x, y) 移动到 (x+A, y+B)。 l 从 (x, y) 移动到 (x+C, y+D)。 l 从 (x, y) 移动到 (x+E, y+F )。

现在在 m 个点 (X1 , Y1), ..., (Xm, Ym) 有障碍物， 小帅不能移动到含有障碍物的点上。在经历了 n 次的移动后会得到多少条路径，答案对于 998244353 进行取模。

34. ①处应填（ ） {{ select(34) }}

• -1
• 1
• 0
• 1e18

35. ②处应填（ ） {{ select(35) }}

• u <= i
• u = i
• u <= n
• u < n

36. ③处应填（ ） {{ select(36) }}

• u+v < i
• u+v <= i
• v+i <= u
• v +i < u

37. ④处应填（ ） {{ select(37) }}

• dp[i][u][v] = (dp[i][u][v]+dp[i-1][u-1][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i][u-1][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i-1][u][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i][u][v]) % mod

38. ⑤处应填（ ） {{ select(38) }}

• i == n
• i
• n
• i == n-1

阅读下面题目，完成第 39~43 题。

给定一个字符串S，有q组询问，每次给定一个字符串T，求字符串T是否是S中的一个子序列。数据保证 ，所有字符串仅包含小写字母。

39. ①处应填（ ） {{ select(39) }}

• Pos[i][n–1]
• Pos[i][n]
• Pos[n–1][i]
• Pos[n][i]

40. ②处应填（ ） {{ select(40) }}

• Pos[i][j] = Pos[i-1][j]
• Pos[i][j] = Pos[i+1][j]
• Pos[i][j] = Pos[i][j–1]
• Pos[i][j] = Po\s[i][j+1]

41. ③处应填（ ） {{ select(41) }}

• Pos[i][S[i]–’a’] = i
• Pos[i][S[i]–’A’] = i
• Pos[i][S[i]] = i
• Pos[i][i] = S[i]

42. ④处应填（ ） {{ select(42) }}

• i < len
• now != -1
• i < len && now != n
• i < len && now != -1

43. ⑤处应填（ ） {{ select(43) }}

• Pos[now][T[i]-‘a’]
• Pos[now][S[i]-‘a’]
• Pos[now+1][T[i]-‘a’]
• Pos[now+1][S[i]-‘a’]