一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项）

1. 八进制数 (7042)8 转化为十六进制数是（ ） {{ select(1) }}

• (3521)16
• (F22)16
• (E22)16
• (111000100010)16

2. 设栈 S 和队列 Q 初始状态为空，元素 a1, a2, ..., a6 依次通过栈 S，一个元素出栈后就进入队列Q，若出队的顺序分别是 a2，a1，a3，a6，a5，a4则栈 S 的容量至少是（ ） {{ select(2) }}

• 2
• 5
• 3
• 4

3. 逻辑表达式（ ）的值与变量 A 的真假无关。 {{ select(3) }}

• (A ∧ B) ∨ (¬A ∧ B)
• (A ∨ B) ∧ ¬A
• (A ∨ B) ∧ ¬B
• (A ∨ B) ∧ ¬A ∧ B

4. n 是一个三位数,那 n 的十位数为（ ）。 {{ select(4) }}

• (n%100)/10
• (n/100)%10
• (n/100)%100
• (n%10)/10

5. 基于比较的排序时间复杂度的下限是（ ），其中 n 表示待排序的元素个数。 {{ select(5) }}

• O(n2)
• O(nlog2n)
• O(n)
• O(log2n)

6. 完全二叉树共有 2 * N-1 个结点，则它的叶节点数是（ ）。 {{ select(6) }}

• N-1
• 2 * N
• 2 * N-1
• N

7. 45 和 30 的最小公倍数是（ ） {{ select(7) }}

• 45
• 30
• 90
• 180

8. 一棵 7 节点二叉树的中序遍历为 ABDGECF ，先序遍历为 DBACEGF ，后序遍历为（ ） {{ select(8) }}

• ABCDEFG
• DGBEFAC
• GBEACFD
• ABGEFCD

9. 一个 n 个顶点的强连通图最少有几条边（ ） {{ select(9) }}

• n
• n+1
• n-1
• n* (n-1)

10. 若有如下程序段，其中 s、a、b、c 均已定义为整型变量，且 a、c 均已赋值（c > 0）

则与上述程序段功能等价的赋值语句是（ ）。 {{ select(10) }}

• s = a - b;
• s = s - c;
• s = a - c;
• s = b - c;

11. 7个人分乘两辆不同的汽车，每辆车最多坐 4 人，则不同的乘车方法数为（ ）。 {{ select(11) }}

• 40
• 50
• 70
• 60

12. 以下关于图的不正确说法是（ ）。 {{ select(12) }}

• 所有顶点的度数之和不一定等于边数的 2 倍
• 所有顶点的度数之和等于边数的 2 倍
• 在有向图中顶点的入度之和等于出度之和
• 任意一个图一定有偶数个度数为奇数的点

13. 定义一个数是 “好的”：当且仅当这个数是个六位数(允许有前导零),并且里面含有数字 9,那么符合“好的”条件的数的个数是（ ）。 {{ select(13) }}

• 531441
• 1000000
• 99999
• 468559

14. 下列叙述中正确的是（ ）。 {{ select(14) }}

• 二叉树是线性结构
• 栈与队列是⾮线性结构
• 线性表是线性结构
• 线性链表是⾮线性结构

15. 现有八人排成一排照相，其中甲乙丙三人两两之间都不能相邻的排法有（ ）种 {{ select(15) }}

• A(6, 3)×A(5, 5)
• A(8, 8)-A(6, 6)×A(3, 3)
• A(5, 3)×A(3, 3)
• A(8, 8)-A(6, 4)

二、阅读程序（程序输入不超过数组或字符串定义的范围；判断题正确填 T，错误填 F；除特殊说明外，判断题1.5 分，选择题 3 分，共计 40 分）

注意：判断题正确填 T ，错误填 F 。

阅读下面程序，完成第16~21题。

16. 将第10 行 res = (res*x)%mod; 和第11 行 x = (x*x)%mod; 的括号去掉，程序输出结果一定不变。（ ） {{ select(16) }}

• 正确
• 错误

17. 将第 12 行的 m>>= 1 改为 mi /= 2 ，程序输出结果一定不变。（ ） {{ select(17) }}

• 正确
• 错误

18. 若输入为 4 4 ，则输出为 78 。（ ） {{ select(18) }}

• 正确
• 错误

19. 此程序的时间复杂度为 O(logn)。（ ） {{ select(19) }}

• 正确
• 错误

20. 若输入为 3 4 ，则输出为（ ）。 {{ select(20) }}

• 18
• 19
• 12
• 8

21. 若输入为 2046 13 的返回值为（ ）。 {{ select(21) }}

• 2024
• 2
• 12
• 2022

阅读下面程序，完成第 22~27 题。

22. 代码中 max_primedivisor = max(max_primedivisor,num); 这句话去掉对答案没有影响。（ ） {{ select(22) }}

• 正确
• 错误

23. 当读入的 num=p*q 其中 p < q ，且 p,q 为质数，则 for 循环中 i 遍历到 q 时退出循环。（ ） {{ select(23) }}

• 正确
• 错误

24. 该算法的最坏时间复杂度为（ ） {{ select(24) }}

• $O(\log_{2}num)$
• $O(\sqrt{num})$
• $O(num)$
• $O(num\sqrt{num})$

25. 当读入 2021 时输出为（ ） {{ select(25) }}

• 43 2
• 43 4
• 47 2
• 47 4

26. 当读入的数 num = p * p * p * q * q * r * r * s * t 时,其中 p<q<r<s<t,且p, r, q, r, s, t 均为质数，则输出的第二个数（ ） {{ select(26) }}

• 144
• 9
• 12
• 不确定

27. 在最好的情况下,时间复杂度为（ ） {{ select(27) }}

• $O(\sqrt{num})$
• $O(num)$
• $O(num\sqrt{num})$
• $O(\log num)$

阅读下面程序，完成第 28 ~33 题。

提示:

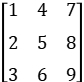
矩阵转置：将第 i 行 ，变为第 i 列，如：

-->

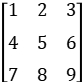矩阵加减法：要保证两个矩阵的 数和列数相同，且相同位置相加减，如：

+ =

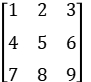矩阵乘法：矩阵A×矩阵B=矩阵C，要保证A的列数和B的行数相同。则Ci,j =Ai,k×Bk,j，如:

x =

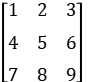28. n, r, c 必须小于 110，否则程序可能会发生运行错误。（ ） {{ select(28) }}

• 正确
• 错误

29. 第 85~88 行不能预防第 x 和第 y 个矩阵不能相加的情况。 {{ select(29) }}

• 正确
• 错误

30. 如果将第 41 行代码修正，则函数 void Multiply(int a, int b) 的功能是计算第 a 个矩阵乘以第 b 个矩阵的结果。（ ） {{ select(30) }}

• 正确
• 错误

31. 第 10 行和第 11 行代码交换位置后，程序运行错误。（ ） {{ select(31) }}

• 正确
• 错误

32. 第 41 行代码是否有误？如果有误，那么正确的代码应该为。（ ） {{ select(32) }}

• 代码正确
• 代码有误；正确代码： Sum[i][j] += G[a].A[i][j] * G[b].A[k][j];
• 代码有误；正确代码： Sum[i][j] += G[a].A[i][k] * G[b].A[k][j];
• 代码有误；正确代码： G[a].A[i][j]+= G[a].A[i][k] * G[b].A[k][j];

33. 若输入：

2 2
3 3
1 2 3
4 5 6
7 8 9
3 3
1 4 7
2 5 6
3 6 9
0 1 2
1 1 2

则正确输出为： {{ select(33) }}

A:
1 2 3
4 5 6
7 6 9
2 6 10
6 10 14

B:
1 4 7
2 5 8
3 6 9
error1

C:
1 4 7
2 5 8
3 6 9
66 64 90
78 77 108
90 90 126

D:
1 4 7
2 5 8
3 6 9
2 6 10
6 10 14
10 12 18

三、完善程序（单选题，每小题3分，共计30分）

阅读下面题目，完成第 34 ~38 题。

输入月份 m(1≤m≤12)，按一定格式打印 2015 第 m 月的月历。例如，2015 年一月的月历打印效果如下（第一列为周日）：

S	M	T	W	T	F	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

34. ①处应填（ ） {{ select(34) }}

• offset=0
• offset=1
• offset=3
• offset=4

35. ②处应填（ ） {{ select(35) }}

• dayNum[i]
• offset+dayNum[i]
• (offset+dayNum[i]) % 7
• (offset+dayNum[i - 1]) % 7

36. ③处应填（ ） {{ select(36) }}

• m
• dayNum[m]
• offset
• offset+dayNum[i]

37. ④处应填（ ） {{ select(37) }}

• i
• i+1
• i - 1
• dayNum[i]

38. ⑤处应填（ ） {{ select(38) }}

• offset+i
• (offset+i) % 7
• offset+dayNum[i]
• (offset+dayNum[i]) % 7

阅读下面题目，完成第 39 ∼ 43 题。

给出一张 n 节点 m 条边的有向图，求出该图的一个拓扑排序，若无拓扑排序输出 −1

输入：第一行两个正整数 n, m 表示点数和边数。接下来 m 行，每行三个正整数 x, y 表示节点 x− > y 之间有一条边。

输出：一个拓扑序：按拓扑序输出点的编号。若拓扑序不唯一，输出任意一个均可。若无拓扑序，输出 −1。

39. 上述程序(1)中应该填写（ ） {{ select(39) }}

• du[i]
• q[i]
• hd <= tl
• !du[i]

40. 上述程序 (2)中应该填写（ ） {{ select(40) }}

• i <= n
• i < n
• i < G[u].size()
• i <= G[u].size()

41. 上述程序 (3) 中应该填写（ ） {{ select(41) }}

• q[++tl] = v
• q[tl++] = v
• q[++hd] = v
• q[hd++] = v

42. 上述程序 (4) 中应该填写（ ） {{ select(42) }}

• G[y].push_back(x)
• G[x].push_back(y)
• G[x].push(y)
• G[y].push(x)

43. 上述程序 (5) 中应该填写（ ） {{ select(43) }}

• G[y].push_back(x)
• G[y].push(x)
• du[y]++
• du[x]++