一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项）

1. 假设 A=TRUE，B=FALSE，C=TRUE，D=TRUE，逻辑运算表达式 A ∧B ∨ C ∧ D 的值是（）： {{ select(1) }}

• TRUE
• 0
• 1
• FALSE

2. 设a[1]=1, a[2]=2, a[3]=3, a[4]=4, a[5]=5, a[6]=6，且 i=1, j=2, k=3, m=4，以下选项中变量值等于 3 的是（ ）： {{ select(2) }}

• a[i * j]
• a[a[j+k - 2]]
• a[a[k - i]+3]
• a[m / j]

3. 八进制数 15264 转换成的二进制数是（ ）： {{ select(3) }}

• 001101010110100
• 101101011010101
• 001011000110100
• 001101010100110

4. 一个二叉搜索树前序遍历的结果为 {7、2、1、5、13、9}，这棵树的根的左子树有多少个节点？（ ）。 {{ select(4) }}

• 2
• 5
• 4
• 3

5. 小明一次可以跨上一阶台阶或两阶台阶。他从第一阶台阶出发，有多少种方案恰好到达第 10 阶台阶？（ ） {{ select(5) }}

• 53
• 55
• 54
• 57

6. 所有满足除以 3 的余数为 2，除以 7 的余数为 1 中，最小的数是 8，第五小的数是（ ）。 {{ select(6) }}

• 40
• 50
• 71
• 92

7. 2021 年 7 月 1 日是星期四，我们热烈庆贺了中国共产党成立一百周年，完成了两个一百年中的第一个。我们将在 2049 年 10 月 1 日欢庆建国一百年，这一天是星期几？（ ）。 {{ select(7) }}

• 星期四
• 星期五
• 星期六
• 星期日

8. 一棵 6 节点二叉树的中序遍历为 DBAGECF ,先序遍历为 ABDCEGF ，后序遍历为（ ）。 {{ select(8) }}

• DGBEFAC
• GBEACFD
• DBGEFCA
• ABCDEFG

9. G 是一张有 n 个点 m 条边的连通图，必须删去（ ）条边才能将其变成一棵 n 节点的树 {{ select(9) }}

• 1
• m-n-1
• m+n-1
• m-n+1

10. 元素 R1、R2、R3、R4、R5 入栈的顺序为 R1、R2、R3、R4、R5。如果第一个出栈的是R3，那么第 5 个出栈的不可能是（ ）。 {{ select(10) }}

• R1
• R2
• R4
• R5

11. 前缀表达式 “+3 * 2 + 5 12” 的值是（ ）。 {{ select(11) }}

• 23
• 25
• 37
• 65

12. 设有 100 个顶点，利用二分法查找时，最大比较次数是（ ） 。 {{ select(12) }}

• 25
• 10
• 7
• 50

13. 十进制小数 13.375 对应的二进制数是（ ）： {{ select(13) }}

• 1101.011
• 1011.011
• 1101.101
• 1010.01

14. 1TB 表示的字节数是（ ）。 {{ select(14) }}

• 2^10
• 2^20
• 2^30
• 2^40

15. 有 18 个表观完全相同的零件，其中有且仅有一个是质量略轻的次品零件。有一个天平，但是没有砝码，可以用于比较左右两个盘中物体的质量。最坏情况下，最少需要多少次称量可以找到这个次品零件？（ ）。 {{ select(15) }}

• 3
• 4
• 6
• 9

二、阅读程序（程序输入不超过数组或字符串定义的范围；判断题正确填 T，错误填 F；除特殊说明外， 判断题1.5 分，选择题 3 分，共计 40 分）

阅读下面程序，完成第 16~21 题。

16. 程序会将读入的字符串中出现次数等于 1 的字符依次输出。（ ） {{ select(16) }}

• 正确
• 错误

17. 将程序中的 for (i = 0; i < 256; i++) t[i] = 0; 删掉可能会影响程序的正确性。（ ） {{ select(17) }}

• 正确
• 错误

18. 当程序读入字符串的内容是 "xyzxyw" 时，程序的输出结果是 w 。（ ） {{ select(18) }}

• 正确
• 错误

19. 对于一组输入数据 "abc?ac" ，如果希望程序的输出结果为 b ，则 ? 处应替换为 b 。（ ） {{ select(19) }}

• 正确
• 错误

20. 若输入的字符串中 a 到 g 这 7 种字符均至少出现一次，如果希望输出结果为 no ，则输入的字符串长度至少为（ ）。 {{ select(20) }}

• 1
• 7
• 14
• 8

21. 这个程序最多正确输入并处理长度为（ ）的字符串 s 。 {{ select(21) }}

• 256
• 15
• 14
• 11

阅读下面程序，完成第 22~27 题。

22. 若输入的 X[1], X[2], ..., X[N ] 中有相同的数,程序会陷入死循环。（ ） {{ select(22) }}

• 正确
• 错误

23. 当且仅当输入的 X[1], X[2], … , X[N ] 全部相同时输出的两行结果相同。（ ） {{ select(23) }}

• 正确
• 错误

24. 该算法的原理是基数排序。（ ） {{ select(24) }}

• 正确
• 错误

25. （4分）若输入的 X[1], X[2], ..., X[N ] 互不相同，则下列说法正确的是（ ） {{ select(25) }}

• 输出的两行结果相同
• 将输出的第一行结果整体翻转后，将与第二行相同
• 将输出的第一行结果的第一项与最后一项交换后，将与第二行相同
• 以上说法都不正确

26. （4分）下列说法不正确的是（ ） {{ select(26) }}

• 输出的第一行即为将 X[1], X[2], ..., X[N ] 从小到大排序后得到的结果
• 输出的第二行即为将 X[1], X[2], ..., X[N ] 从大到小排序后得到的结果
• 若将 a[i]> a[j] 改为 a[i] >=a[j] ，则程序输出无变化
• 不存在时间复杂度更优的能与本程序达到相同目的的算法

27. 该程序的时间复杂度为（ ） {{ select(27) }}

• O(nlogn)
• O(n)
• O(n^2)
• O(n * √n )

阅读下面程序，完成第28~33题。

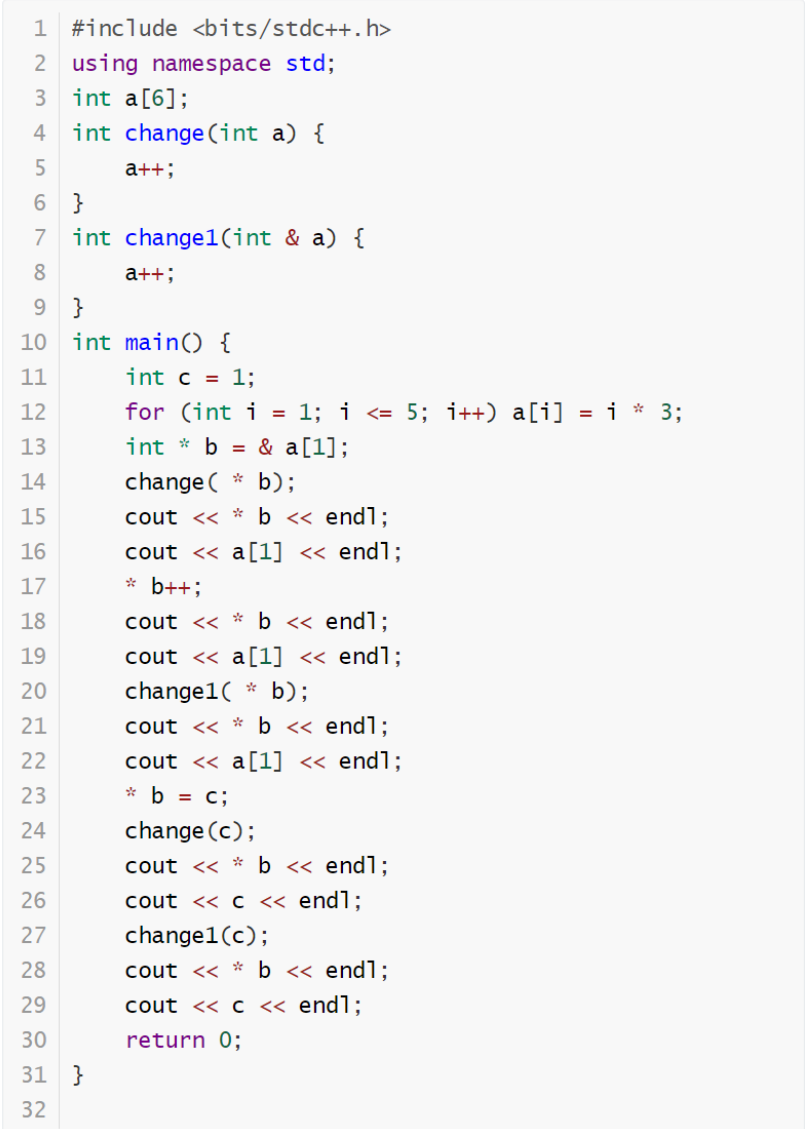
28. 将 int c = 1; 中 int 换为 long long 后程序依然能通过编译。（ ） {{ select(28) }}

• 正确
• 错误

29. change 与 change1 两个函数等价。（ ） {{ select(29) }}

• 正确
• 错误

30. 将 * b = c; 换为 b = &c; 输出值不变。（ ） {{ select(30) }}

• 正确
• 错误

31. 将 int * b = & a[1]; 换为 int * b=a+1; 输出值不变。（ ） {{ select(31) }}

• 正确
• 错误

32. 输出结果的最大值是。（ ） {{ select(32) }}

• 6
• 4
• 7
• 5

33. 输出结果的乘积是。（ ） {{ select(33) }}

• 13608
• 11520
• 5760
• 6804

三、完善程序（单选题，每小题3分，共计30分）

阅读下面题目，完成第 34 ∼ 38 题。

小帅目前处在一个二维平面上，初始状态下小帅在原点 (0, 0)。小帅会进行 n 次如下的移动，每次移动小帅有三种选择：

l 从 (x, y) 移动到 (x+A, y+B)。 l 从 (x, y) 移动到 (x+C, y+D)。 l 从 (x, y) 移动到 (x+E, y+F )。

现在在 m 个点 (X1 , Y1), ..., (Xm, Ym) 有障碍物， 小帅不能移动到含有障碍物的点上。在经历了 n 次的移动后会得到多少条路径，答案对于 998244353 进行取模。

34. ①处应填（ ） {{ select(34) }}

• -1
• 1
• 0
• 1e18

35. ②处应填（ ） {{ select(35) }}

• u <= i
• u = i
• u <= n
• u < n

36. ③处应填（ ） {{ select(36) }}

• u+v < i
• u+v <= i
• v+i <= u
• v +i < u

37. ④处应填（ ） {{ select(37) }}

• dp[i][u][v] = (dp[i][u][v]+dp[i-1][u-1][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i][u-1][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i-1][u][v]) % mod
• dp[i][u][v] = (dp[i][u][v]+dp[i][u][v]) % mod

38. ⑤处应填（ ） {{ select(38) }}

• i == n
• i
• n
• i == n-1

阅读下面题目，完成第 39~43 题。

给定一个字符串S，有q组询问，每次给定一个字符串T，求字符串T是否是S中的一个子序列。数据保证 ，所有字符串仅包含小写字母。

39. ①处应填（ ） {{ select(39) }}

• Pos[i][n–1]
• Pos[i][n]
• Pos[n–1][i]
• Pos[n][i]

40. ②处应填（ ） {{ select(40) }}

• Pos[i][j] = Pos[i-1][j]
• Pos[i][j] = Pos[i+1][j]
• Pos[i][j] = Pos[i][j–1]
• Pos[i][j] = Po\s[i][j+1]

41. ③处应填（ ） {{ select(41) }}

• Pos[i][S[i]–’a’] = i
• Pos[i][S[i]–’A’] = i
• Pos[i][S[i]] = i
• Pos[i][i] = S[i]

42. ④处应填（ ） {{ select(42) }}

• i < len
• now != -1
• i < len && now != n
• i < len && now != -1

43. ⑤处应填（ ） {{ select(43) }}

• Pos[now][T[i]-‘a’]
• Pos[now][S[i]-‘a’]
• Pos[now+1][T[i]-‘a’]
• Pos[now+1][S[i]-‘a’]